Una sinfonía matemática en la naturaleza
Gerson D. Alducin Chávez

La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras, y el otro la división de una línea en la proporción del medio y los extremos, es decir el número áureo. El primero puede compararse a una medida de oro, y el segundo a una piedra preciosa
Johannes Kepler
El Misterio Cósmico
En los rincones más internos de la naturaleza coexiste una armonía matemática que transcurre silenciosa, como una sinfonía que solo los observadores más audaces pueden percibir; es en el centro de esta sinfonía donde el número áureo y la serie de Fibonacci se entrelazan, creando una composición matemática que se proyecta en la estructura misma de la vida. Esta conexión entre el número áureo y la serie de Fibonacci revela una fascinante representación matemática que se manifiesta de maneras asombrosas en el reino biológico.

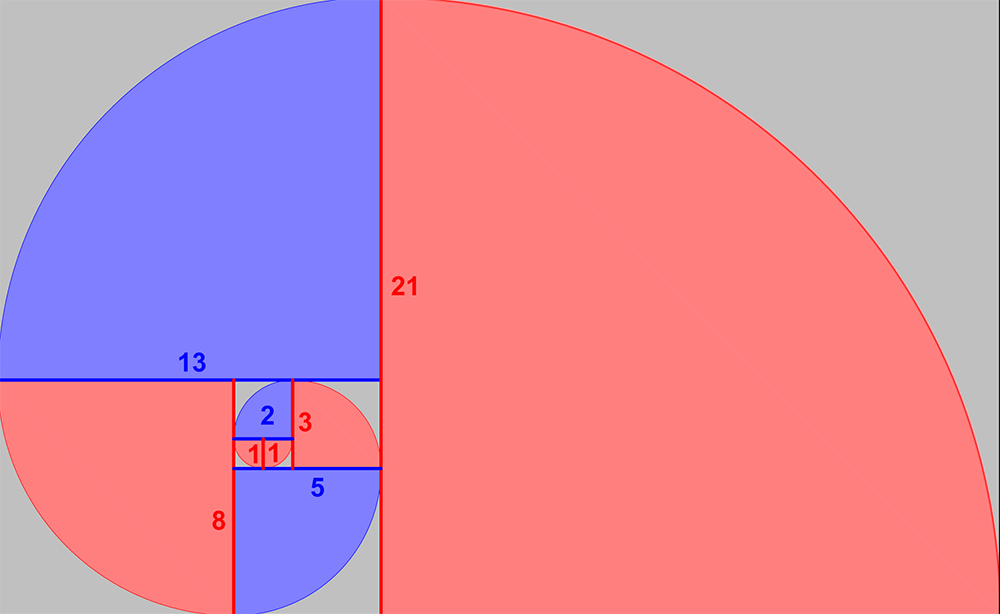
Espiral de Fibonacci construida a partir de rectángulos
El número áureo, representado por la letra griega φ (phi), es una constante matemática que ha atrapado la imaginación de artistas, científicos y filósofos a lo largo de la historia, desde Euclides (c. 300–265 a.C.) hasta nuestros tiempos. Además de ser un dato numérico, es la esencia misma de proporciones estéticas y equilibrio visual, su valor se aproxima a 1.618. Por su parte, la serie de Leonardo il Fibonacci (c. 1170–1240 d.C.) es una secuencia numérica donde cada elemento es la suma de los dos anteriores (0, 1, 1, 2, 3, 5, 8, 13, ...); se podría decir que es la compañera natural del número áureo. La relación entre números sucesivos de esta serie converge hacia el número áureo a medida que avanzamos en la secuencia. Esta unión matemática entre el número áureo y la serie Fibonacci es una expresión inherente a la naturaleza.
De esta manera, la relación entre el número áureo y la sucesión de Fibonacci se expresa en la disposición de hojas en las plantas; por ejemplo en los girasoles y helechos, en la distribución de pétalos en las flores y en innumerables patrones del mundo vegetal. Si contáramos el número de espirales en direcciones opuestas, a menudo encontraremos que estos números son consecutivos en la serie de Fibonacci; esta disposición optimizada permite una exposición máxima al sol y un eficiente uso del espacio, con lo que se evidencia cómo la matemática establece la arquitectura de las flores.


En los animales, la proporción áurea se muestra en la disposición de las escamas en ciertos reptiles, en los cuernos del borrego cimarrón y en la distribución de las alas de mariposas. Las formas y patrones que siguen las proporciones áureas y la serie de Fibonacci podrían proporcionar una distribución de recursos más efectiva. Cada rama, cada pétalo, y cada escama son notas en esta sinfonía matemática que resuena en la naturaleza, recordándonos que las leyes de la matemática no son solo abstracciones, sino la partitura que guía la danza elegante de la vida.
“La opinión es responsabilidad de los autores y no representa una postura institucional”
